November 22, 2011
November 16, 2011
November 11, 2011
November 08, 2011
November 07, 2011
ANGLE OF REPOSE
The angle of repose or, more precisely, the critical angle of repose,[1] of a granular material is the steepest angle of descent or dip of the slope relative to the horizontal plane when material on the slope face is on the verge of sliding. This angle is in the range 0°–90°.
When bulk granular materials are poured onto a horizontal surface, a conical pile will form. The internal angle between the surface of the pile and the horizontal surface is known as the angle of repose and is related to the density, surface area and shapes of the particles, and the coefficient of friction of the material. Material with a low angle of repose forms flatter piles than material with a high angle of repose.
The term has a related usage in mechanics, where it refers to the maximum angle at which an object can rest on an inclined plane without sliding down. This angle is equal to the arctangent of the coefficient of static friction μs between the surfaces.
When bulk granular materials are poured onto a horizontal surface, a conical pile will form. The internal angle between the surface of the pile and the horizontal surface is known as the angle of repose and is related to the density, surface area and shapes of the particles, and the coefficient of friction of the material. Material with a low angle of repose forms flatter piles than material with a high angle of repose.
The term has a related usage in mechanics, where it refers to the maximum angle at which an object can rest on an inclined plane without sliding down. This angle is equal to the arctangent of the coefficient of static friction μs between the surfaces.
November 04, 2011
INCLINED PLANE
Inclined Planes
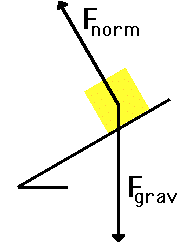An
object placed on a tilted surface will often slide
down the surface. The rate at which the object slides down
the surface is dependent upon how tilted the surface
is; the greater the tilt of the surface, the faster
the rate at which the object will slide down it. In physics,
a tilted surface is called an inclined plane. Objects
are known to accelerate down inclined planes because of an
unbalanced force. To understand this type of motion, it is
important to analyze the forces acting upon an object on an
inclined plane. The diagram at the right depicts the two
forces acting upon a crate that is positioned on an
inclined plane (assumed to be friction-free). As shown in
the diagram, there are always at least two forces
acting upon any object that is positioned on an inclined
plane - the force of gravity and the normal force. The
force of gravity (also
known as weight) acts in a downward direction; yet the
normal force acts in a
direction perpendicular to the surface (in fact,
normal means "perpendicular").The first peculiarity of inclined plane problems is that the normal force is not directed in the direction that we are accustomed to. Up to this point in the course, we have always seen normal forces acting in an upward direction, opposite the direction of the force of gravity. But this is only because the objects were always on horizontal surfaces and never upon inclined planes. The truth about normal forces is not that they are always upwards, but rather that they are always directed perpendicular to the surface that the object is on.
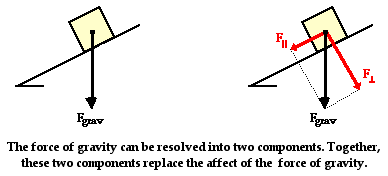
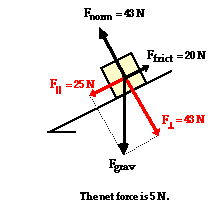(in the absence of friction and
other forces)
In
the presence of friction or other forces (applied force,
tensional forces, etc.), the situation is slightly more
complicated. Consider the diagram shown at the right. The
perpendicular component of force still balances the normal
force since objects do not accelerate perpendicular to the
incline. Yet the frictional force must also be considered
when determining the net force. As in all net force
problems, the net force
is the vector sum of all the forces. That is, all the
individual forces are added together as vectors. The
perpendicular component and the normal force add to 0 N. The
parallel component and the friction force add together to
yield 5 N. The net force is 5 N, directed along the incline
towards the floor.The above problem (and all inclined plane problems) can be simplified through a useful trick known as "tilting the head." An inclined plane problem is in every way like any other net force problem with the sole exception that the surface has been tilted. Thus, to transform the problem back into the form with which you are more comfortable, merely tilt your head in the same direction that the incline was tilted. Or better yet, merely tilt the page of paper (a sure remedy for TNS - "tilted neck syndrome" or "taco neck syndrome") so that the surface no longer appears level. This is illustrated below.
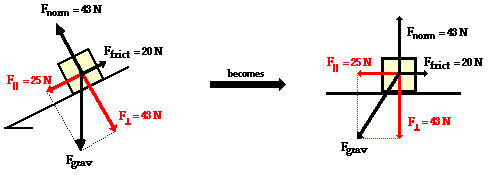
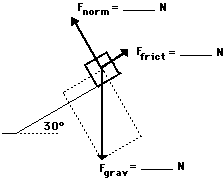As
an example consider the situation depicted in the diagram at
the right. The free-body diagram shows the forces acting
upon a 100-kg crate that is sliding down an inclined plane.
The plane is inclined at an angle of 30 degrees. The
coefficient of friction between the crate and the incline is
0.3. Determine the net force and acceleration of the
crate.Begin the above problem by finding the force of gravity acting upon the crate and the components of this force parallel and perpendicular to the incline. The force of gravity is 980 N and the components of this force are Fparallel = 490 N (980 N • sin 30 degrees) and Fperpendicular = 849 N (980 N • cos30 degrees). Now the normal force can be determined to be 849 N (it must balance the perpendicular component of the weight vector). The force of friction can be determined from the value of the normal force and the coefficient of friction; Ffrict is 255 N (Ffrict = "mu"*Fnorm= 0.3 • 849 N). The net force is the vector sum of all the forces. The forces directed perpendicular to the incline balance; the forces directed parallel to the incline do not balance. The net force is 235 N (490 N - 255 N). The acceleration is 2.35 m/s/s (Fnet/m = 235 N/100 kg).
Practice
The two diagrams below depict the free-body diagram for a
1000-kg roller coaster on the first drop of two different
roller coaster rides. Use the above principles of vector
resolution to determine the net force and acceleration of
the roller coaster cars. Assume a negligible affect of
friction and air resistance. When done, click the button to
view the answers.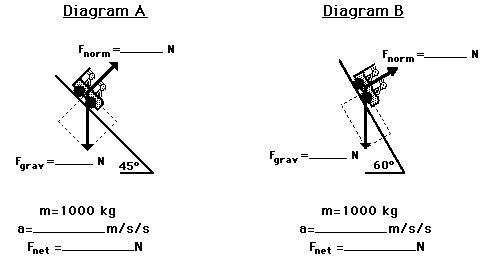
The affects of the incline angle on the acceleration of a roller coaster (or any object on an incline) can be observed in the two practice problems above. As the angle is increased, the acceleration of the object is increased. The explanation of this relates to the components that we have been drawing. As the angle increases, the component of force parallel to the incline increases and the component of force perpendicular to the incline decreases. It is the parallel component of the weight vector that causes the acceleration. Thus, accelerations are greater at greater angles of incline. The diagram below depicts this relationship for three different angles of increasing magnitude.
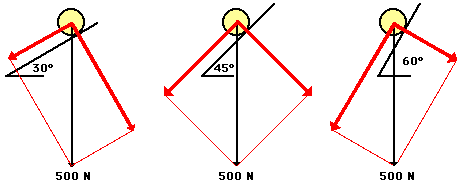
Roller
coasters produce two thrills associated with the initial
drop down a steep incline. The thrill of acceleration is
produced by using large angles of incline on the first drop;
such large angles increase the value of the parallel
component of the weight vector (the component that causes
acceleration). The thrill of weightlessness is
produced by reducing the magnitude of the normal force to
values less than their usual values. It is important to
recognize that the thrill of weightlessness is a feeling
associated with a lower than usual normal force. Typically,
a person weighing 700 N will experience a 700 N normal force
when sitting in a chair. However, if the chair is
accelerating down a 60-degrees incline, then the person will
experience a 350 Newton normal force. This value is less
than normal and contributes to the feeling of weighing less
than one's normal weight - i.e.,
weightlessness.Angles of Friction
Equations
Nomenclature
| symbol | description |
| φs | angle of static friction |
| φk | angle of kinetic friction |
| μs | coefficient of static friction |
| μk | coefficient of kinetic friction |
| N | normal component of the reaction surface |
Explanation
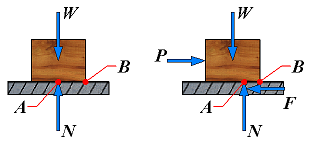
It is sometimes convenient to replace the normal force N and the friction force F by a resultant R. Consider a block of weight W resting on a horizontal plane surface:
| No friction | R = N | 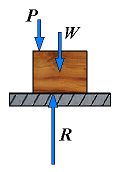 | If no horizontal force is applied to the block, the resultant R reduces to the normal force N. |
| No motion | F = Px φ < φs | 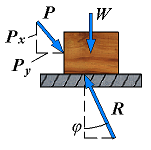 | However, if the applied force P has a horizontal component Px which tends to move the block, the force R will have a horizonatal component F and, thus, will form an angle φ with the normal to the surface as shown. |
| Motion impending | Fm = Px φ = φs | 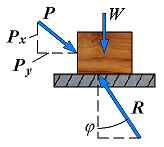 | If Px is increased until motion becomes impending, the angle between R and the vertical grows and reaches a maximum value. |
This maximum value is called the angle of static friction and is denoted by φs. From the geometry of the previous figure, the equation is:
| tan φs = |
| = |
|
| tan φs = μs |
| Motion | F = Px φ < φs | 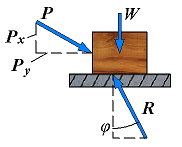 | If motion actually takes place, the magnitudes of the friction force drops to Fk; similarly, the angle φ between R and N drops to a lower value φk, called the angle of kinetic friction. |
From the geometry of the previous figure, the equation is:
| tan φk = |
| = |
|
| tan φk = μk |
Another example may show how the angle of friction can be used to advantage in the analysis of certain types of problems. Consider a block resting on a base and subjected to no other force than its weight W and the reaction R of the board. The board can be given any desired inclination.
| No friction | R = N | 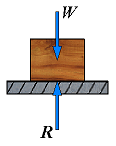 | If the base is horizontal, the force R exerted by the board on the block is perpendicular to the base and balances the weight W. |
| No motion | F = Px φ < φs | 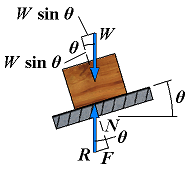 | If the base is given a small angle of inclination, θ, the force R will deviate from the perpendicular to the base by the angle θ and will keep balancing W; it will then have a normal componenet N of magnitude N = W cos θ and a tangential component F of magnitude F = W sin θ. |
| Motion impending | Fm = Px φ = φs | 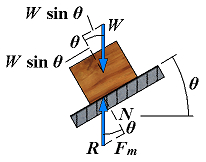 | If the angle of inclination continues to increase, motion will soon become impending. At that time, the angle between R and the normal will have reached its maximum value φs. The value of the angle of inclination corresponding to impending motion is called the angle of repose. Clearly, the angle of repose is equal to the angle of static friction φ. |
| Motion impending | Fm = Px φ = φs | 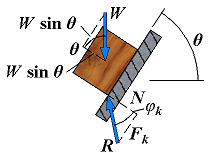 | If the angle of inclination θ is further increased, motion starts and the angle between R and the normal drops to the lower value φk. The reaction R is not vertical any more, and the forces acting on the block are unbalanced. |
LAWS OF FRICTION
| Laws of Dry Friction and Coefficients of Friction |
Equations
| Magnitude of the maximum static friction force | ||
| Magnitude of the kinetic friction force |
Nomenclature
| symbol | description |
| Fm | maximum force |
| Fk | kinetic friction force |
| μs | coefficient of static friction |
| μk | coefficient of kinetic friction |
| N | normal component of the reaction surface |
Explanation
Friction is both good and bad: it allows objects to move, such as in walking or driving, yet can result in a lot of wasted energy through the generation of heat, such as in engines, and in other areas.
Friction can be understood simply by observing the following picture of a cinder block sitting on asphalt:
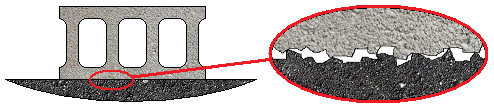
Zooming in, it can be seen that there are irregularities in the surfaces of both materials, and when they are moved against each other, these small bits are pushing against each other. It is the summation of all of these horizontal forces causing resistance that make it hard to push an object with a lot of friction. When an object is pushed the bits may break off, or they may bump over each other. The weight of the object, or any vertical forces that are pushing down on the object, will influence the friction because as vertical downward force is increased, it becomes harder to overcome those horizontal forces between all the little small bits interconnected with each other between the contacting surfaces.
The laws of dry friction may be explained with a wooden block of weight W that is placed on a horizontal concrete plane surface as shown below.
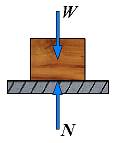
The forces acting on the block are its weight W and the reaction of the surface. Since the weight has no horizontal component, the reaction of the surface also has no horizontal component. The reaction is therefore normal to the surface and is represented by N as shown above.
Now a horizontal force P is applied to the block as shown in the following figure:
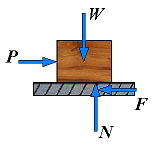
If P is small enough, the block will not move. This only means that some other horizontal force must therefore exist, which balances P. This other force is the static-friction force F, which is actually the resultant of numerous forces acting over the entire surface of contact between the block and the plane, as indicated in the first picture in this lesson. It is generally assumed that these forces are due to the irregularities of the surfaces in contact and, to a certain extent, to molecular attraction.
If the force P is increased, the friction force F also increases, continuing to oppose P until its magnitude reaches a certain maximum value Fm, as shown in the following plot:
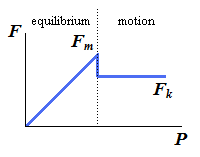
If P is further increased, the friction force cannot balance it any more and the block starts sliding. A more accurate representation of the previous plot may be the following:
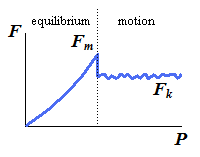
F and P are relatively proportional until Fm is reached, and motion begins. Fk may be shown as a wavy and bumpy line because the frictional force varies at the micro-level interactions, as seen in the first picture in this lesson, which may not be consistent.
Notice in the following figure that, as the magnitude F of the friction force increases from 0 to Fm, the point of application a of the resultant N of the normal forces of contact moves to the right, so that the couples formed, respectively, by P and F and by W and N remain balanced.
If N reaches point b, which is fixed at the bottom corner of the block, before F reaches its maximum value Fm, the couples will no longer be balanced and the block will tip about point b before the block can start sliding.
As soon as the block has been set in motion, the magnitude of F drops from Fm to a lower value Fk as shown below and in the above plots:
This is because there is less interpenetration between the irregularities of the surfaces in contact when these surfaces move with respect to each other. From then on, the block keeps sliding with increasing velocity while the friction force is now denoted by Fk, which is called the kinetic friction force. This can be observed in the plot above. The kinetic friction force remains approximately constant throughout the motion of the block.
Experimental evidence shows that the maximum value Fm of the static friction force is proportional to the normal component N of the reaction of the surface. The equation is:
| (Eq1) |
|
Where μs is a constant called the coefficient of static friction. Similarly, the magnitude Fk of the kinetic friction force may be put in the form:
| (Eq2) |
|
Where μk is a constant called the coefficient of kinetic friction. The coefficients of friction μs and μk do not depend upon the area of the surfaces in contact. Both coefficients, however, depend strongly on the nature of the surfaces in contact. Since they also depend upon the exact condition of the surfaces, their value is seldom known with an accuracy greater than 5 percent. The corresponding values of the coefficient of kinetic friction would be about 25 percent smaller.
It is presumed that four different situations can occur when a rigid body is in contact with a horizontal surface:
| 1. | No friction (Px = 0) | F = 0 N = P + W | 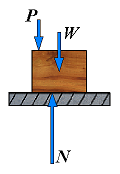 | The forces applied to the body do not tend to move it along the surface of contact; there is not friction force. |
| 2. | No motion (Px < Fm) | F = Px F < μsN N = Py + W | 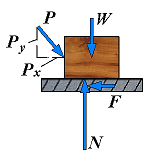 | The applied forces tend to move the body along the surface of contact but are not large enough to set it in motion. The friction force F which has developed can be found by solving the equations of equilibrium for the body. Since there is no evidence that F has reached its maximum value, the equation Fm = μsN cannot be used to determine the friction force. |
| 3. | Motion impending (Px = Fm) | Fm = Px Fm = μsN N = Py + W | 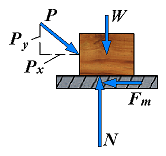 | The applied forces are such that the body is just about to slide, that is, motion is impending. The friction force F has reached its maximum value Fm and, together with the normal force N, balances the applied forces. Both the equations of equilibrium and the equation Fm = μsN can be used. Also note that the friction force has a sense opposite to the sense of impending motion. |
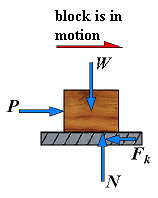
| 4. | Motion (Px > Fm) | Fk < Px Fk = μkN N = Py + W | 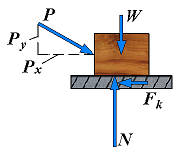 | The body is sliding under the action of the applied forces, and the equations of equilibrium do not apply any more. However, F is now equal to Fk and the equation Fk = μkN may be used. The sense of Fk is opposite to the sense of motion. |
November 03, 2011
Fwd: UK University of Leicester Open Scholarships | Fellowships for Women from Developing Countries | More Apply Today
---------- Forwarded message ----------
From: Scholarship Positions <admin@scholarship-positions.com>
Date: Wed, Nov 2, 2011 at 9:59 PM
Subject: UK University of Leicester Open Scholarships | Fellowships for Women from Developing Countries | More Apply Today
To: cavinojijo@gmail.com
![Your Scholarship Application from Scholarship Positions]()
From: Scholarship Positions <admin@scholarship-positions.com>
Date: Wed, Nov 2, 2011 at 9:59 PM
Subject: UK University of Leicester Open Scholarships | Fellowships for Women from Developing Countries | More Apply Today
To: cavinojijo@gmail.com
New College Scholarships and Financial Aid Updates from Scholarship-Positions.com Please find recently updated scholarships on Scholarship-Positions.com. Help Others: Please forward this email to your friends if they are also interested in scholarships. UK's University of Leicester Open Scholarships for International Students University of Leicester is one of the best universities of the UK. University of Leicester have announced a wide range.. [Read Full Scholarship Detail]
Dorothy Senesh Fellowship for Women from Developing Countries, USA 2012 Graduate Fellowship in Peace and Development Studies for Women from Developing Countries, USA Study Subject(s):Peace and Development Studies Course Level:Graduate.. [Read Full Scholarship Detail]
University of Warwick, UK, Scholarships for International Students Warwick University is one of the UK's leading universities, with a reputation for excellence and a vision to further improve.. [Read Full Scholarship Detail]
Graduate Courses Scholarships at the University of Oxford for International Students All applicants for graduate study at the University of Oxford are eligible. Clarendon scholars come from all continents in the world. .. [Read Full Scholarship Detail] 2012 TWAS-UNICAL Fellowship for Master's Students, China The University of Calabria (UNICAL), Italy, and TWAS announce TWAS-UNICAL Fellowship for Master's Students in the areas of pharmacology/nutrition, China.. [Read Full Scholarship Detail]
2012 Toyota Earth Day Scholarship Program, Canada Scholarships for Canadian Students Graduating from a Canadian High School or Quebec Cégep, Canada 2012 Study Subject(s):Courses offered by the.. [Read Full Scholarship Detail]
2012 EADA funded Scholarship for MBA Programme, Spain Master's Scholarship for Business Administration (MBA) Students in Spain 2012 Study Subject(s):MBA Course Level:Master's Scholarship Provider: EADA Scholarship can be.. [Read Full Scholarship Detail]
VIB International PhD Program in Life Sciences at Flanders, Belgium 2012 PhD scholarships for international life sciences students at VIB, a life sciences research institute in Flanders, Belgium Study Subject(s):life sciences.. [Read Full Scholarship Detail]
Ohio First STEM Scholarship at University of Akron, USA 2012 Bachelor's Scholarship in Science, Technology, Engineering and Mathematics for USA students at University of Akron, USA 2012 Study Subject(s):Science, Technology,.. [Read Full Scholarship Detail]
Dorabji TATA Scholarship The J.N. Tata Endowment was set up in 1892 by the Founder of the Tata group, Jamsetji N. Tata, to.. [Read Full Scholarship Detail]
2012-2013 The Refractories Institute (TRI) Scholarship Program, USA Undergraduate and Graduate Scholarship in Refractory Manufacturing for North American students at Refractories Institute, USA 2012 Study Subject(s):Ceramic Engineering, Materials.. [Read Full Scholarship Detail]
Ross Waite Parsons Scholarship at University of Sydney, Australia Postgraduate Research Scholarship in Law at University of Sydney, Australia 2011 Study Subject(s):Law Course Level:Postgraduate Research Scholarship Provider: Sydney Law.. [Read Full Scholarship Detail]
2012 Asthma Research PhD Scholarship, Australia PhD Scholarship in Medical Sciences, Clinical, Psychological or Consumer Investigation at any University in Australia 2012 Study Subject(s):Asthma (Medical Sciences, Clinical,.. [Read Full Scholarship Detail]
MEAFA Top-Up PhD Research Scholarship at University of Sydney, Australia Postgraduate Research Scholarship in Humanities & Social Sciences at University of Sydney, Australia 2011 Study Subject(s):Humanities & Social Sciences Course.. [Read Full Scholarship Detail]
2012 LMSA Scholarship for USA Medical Students, USA Undergraduate Scholarship for USA Medical Students to study at any USA Medical Schools 2012 Study Subject(s):Medical Course Level:Undergraduate Scholarship Provider:.. [Read Full Scholarship Detail]
WITAN President's Scholarship at University of Akron, USA 2012 Undergraduate and Graduate Scholarship for Female Nontraditional Student at University of Akron, USA 2012 Study Subject(s):Courses offered by the University.. [Read Full Scholarship Detail]
2012 TWAS-CAS Postdoctoral Fellowship for Developing Countries Applicants, China Postdoctoral Fellowship for Developing Countries Students in the field of the natural sciences, China- 2012 Study Subject(s):Natural sciences Course Level:Postdoctoral.. [Read Full Scholarship Detail]
2012 TWAS-icipe Fellowships for Visiting Scholars in Kenya The International Centre of Insect Physiology and Ecology (icipe), Nairobi, Kenya, and TWAS offer one fellowship for visiting scholars from.. [Read Full Scholarship Detail]
Research Position in Mathematics at National Institute of Technology, India The Department of Mathematics of the Institute offers Research Position in Mathematics at National Institute of Technology, India Study Subject(s):Fuzzified.. [Read Full Scholarship Detail]
Junior Research Fellowship at Indian Agricultural Research Institute, India BRNS funded Junior Research Fellowship in Molecular characterization of Triticum dicoccum-derived rust resistance wheat lines and reducing the linkage drag.. [Read Full Scholarship Detail]
Senior Research Fellowship at Water Technology Centre, IARI, India SRF Position in Decision Support System for Enhancing Productivity in Irrigated Saline Environment using Remote Sensing, Modeling and GIS at.. [Read Full Scholarship Detail]
RA and SRF Position in Environmental Sciences at IARI, India Research Position in the Division of Environmental Sciences at Indian Agricultural Research Institute, India Study Subject(s):National Initiative of Climate Resilient.. [Read Full Scholarship Detail]
PhD Studentships in Ultrafast Imaging and Structural Dynamics, Germany PhD Studentships in Ultrafast Imaging and Structural Dynamics at the University of Hamburg, Germany 2012 Study Subject(s):Ultrafast Imaging and Structural.. [Read Full Scholarship Detail]
2012-2013 TWAS-CSIR Postgraduate Fellowship Programme, India Postgraduate Fellowships for foreign scholars from Developing countries in Science and technology, Study Subject(s):Science and technology Course Level:Postgraduate Fellowships Scholarship Provider: TWAS-CSIR.. [Read Full Scholarship Detail]
Postdoctoral Fellowship Position in Nursing at Tshwane University of Technology, South Africa 2011/2012 Postdoctoral Fellowship in Nursing at Adelaide Tambo School of Nursing Science , Tshwane University of Technology, South Africa Study Subject(s):Nursing Science Course.. [Read Full Scholarship Detail]
MSc in Latin American Studies Scholarships, University of Oxford, UK CAF-Latin American Development Bank and the Latin American Centre, University of Oxford, invite applications for two scholarships to study for.. [Read Full Scholarship Detail]
Masters Scholarships 2012 in Applied Sciences at Saint Mary's University, Canada Scholarships 2012 for M.Sc Students at Saint Mary's University, Canada Study Subject(s):Applied Sciences Course Level:Masters Scholarship Provider: Saint Mary's University.. [Read Full Scholarship Detail]
PhD Fellowships in Continental Lithosphere at University of Copenhagen, Denmark 2 PhD fellowships in Continental Lithosphere at the Department of Geography and Geology at University of Copenhagen, Denmark 2011 Study Subject(s):Continental Lithosphere.. [Read Full Scholarship Detail]
Postgraduate Scholarship in Smart Grids at University of Sydney, Australia Postgraduate Research Scholarship in Sciences & Engineering at University of Sydney, Australia 2011 Study Subject(s):Sciences & Engineering Course Level:Postgraduate Research.. [Read Full Scholarship Detail]
PhD Position in Quaternary Geology at Stockholm University, Sweden 2011 PhD Position in Quaternary Geology at the Department of Physical Geography and Quaternary Geology in Stockholm University, Sweden 2011 Study.. [Read Full Scholarship Detail]
PhD Research in Biogeochemistry/ Paleoclimatology at Utrecht University, Netherlands PhD Research in the Nutrient-climate Connection in a Greenhouse world: reading Ancient SedimentRecords at Utrecht University, Netherlands Study Subject(s):Biogeochemistry/Paleoclimatology Course.. [Read Full Scholarship Detail]
Postdoctoral Fellowship in Life Science at University of Copenhagen, Denmark 2011 Postdoctoral Fellowship in Life Science in the Lund Group at BRIC, University of Copenhagen, Denmark 2011 Study Subject(s):Life Science Course.. [Read Full Scholarship Detail]
Reca Stone Scholarship in Legal Theory at University of Sydney, Australia 2011 Postgraduate Research Scholarship in Legal Theory at University of Sydney, Australia 2011 Study Subject(s):Humanities & Social Sciences Course Level:Postgraduate Research.. [Read Full Scholarship Detail]
John O'Brien Memorial Research Scholarship at University of Sydney, Australia 2011 Postgraduate Research Scholarship in Criminal Law and Criminology at University of Sydney, Australia 2011 Study Subject(s):Criminal Law and Criminology Course.. [Read Full Scholarship Detail]
Postdoctoral Research Fellowship in Eddy-resolving Simulations for Turbomachinery , UK 2012 Postdoctoral Research Fellowship in Eddy-resolving Simulations for Turbomachinery at University of Southampton , UK Study Subject(s):Eddy-resolving Simulations for Turbomachinery.. [Read Full Scholarship Detail]
Clark Fletcher Memorial Citrus Bursary at University of Canterbury, New Zealand International Undergraduate and Postgraduate Bursary in Forestry at University of Canterbury, New Zealand 2011 Study Subject(s):Forestry Course Level:Undergraduate, Postgraduate Scholarship Provider:.. [Read Full Scholarship Detail]
Postdoctoral Research Position in Ecosystem Services and Transport Fuels, UK 2011 Postdoctoral Research Position in Ecosystem Services and Transport Fuels in Imperial College London, Department of Earth Science and Engineering at.. [Read Full Scholarship Detail]
Stan and Jean Perron Awards at Curtin University, Australia 2012 Merit Based Research Awards in Health Sciences for Australian Citizens at Curtin University, Australia 2012 Study Subject(s):Health Sciences Course Level:Research Scholarship.. [Read Full Scholarship Detail]
Postdoctoral Position in Astrophysics and Planetary Science, Israel, 2012 Postdoctoral position in astrophysics and planetary science by joint astrophysics group in the Haifa area, Israel Study Subject(s):Astrophysics and Planetary.. [Read Full Scholarship Detail]
Postdoctoral Research Associate in Molecular Biology at Konkuk University, Korea Postdoctoral Research Associate Position, Dept. of Molecular Biology at Konkuk University, Korea 2012 Study Subject(s):Molecular Biology Course Level:Postdoctoral Scholarship Provider:.. [Read Full Scholarship Detail]
Postdoctoral Position in Application Protocol Programming in a CyberOPC Project, Brazil
Looking for More Scholarships? Thousands of students worldwide are searching scholarships on Scholarship-Positions.com, visit oursite for recent scholarship news. Cheers, Amit Kumar Singh International Student Adviser Scholarship-Positions.com Team |
Useful Links Academic Jobs in India Free GRE Prep Jobs in Africa | ||||||||||||||||||||||||||||||
Scholarship-Positions.com Scholarship-Positions.com International Scholarships and Financial Aid Information Services Office: 106 Civil Lines, Church Road, Bareilly, India, 243005 | |||||||||||||||||||||||||||||||
| To unsubscribe or change subscriber options visit: http://www.aweber.com/z/r/?7AzMDCxMtKwMjGysjMzMtEa0jEzMrAyMjGw= |
Subscribe to:
Posts (Atom)