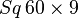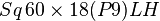The term "Mie theory" is used on occasion but it is misleading, since it does not refer to an independent physical theory or law. The phrase "the Mie solution (to Maxwell's equations)" is therefore preferable. Currently, the term "Mie solution" is also used in broader contexts, for example when discussing solutions of Maxwell's equations for scattering by stratified spheres or by infinite cylinders, or generally when dealing with scattering problems solved using the exact Maxwell equations in cases where one can write separate equations for the radial and angular dependence of solutions.
A modern formulation of the Mie solution to the scattering problem on a sphere can be found in many books, e.g., in J. A. Stratton's Electromagnetic Theory.[1] In this formulation, the incident plane wave as well as the scattering field is expanded into radiating spherical vector wave functions. The internal field is expanded into regular spherical vector wave functions. By enforcing the boundary condition on the spherical surface, the expansion coefficients of the scattered field can be computed.
For particles much larger or much smaller than the wavelength of the scattered light there are simple and excellent approximations that suffice to describe the behaviour of the system. But for objects whose size is similar to the wavelength (e.g., water droplets in the atmosphere, latex particles in paint, droplets in emulsions including milk, and biological cells and cellular components) this more exact approach is necessary.[2]
The Mie solution[3] is named after its developer, German physicist Gustav Mie. Danish physicist Ludvig Lorenz and others independently developed the theory of electromagnetic plane wave scattering by a dielectric sphere.
The formalism allows the calculation of the electric and magnetic fields inside and outside a spherical object and is generally used to calculate either how much light is scattered, the total optical cross section, or where it goes, the form factor. The notable features of these results are the Mie resonances, sizes that scatter particularly strongly or weakly.[4] This is in contrast to Rayleigh scattering for small particles and Rayleigh–Gans–Debye scattering (after Lord Rayleigh, R. Gans and Peter Debye) for large particles. The existence of resonances and other features of Mie scattering, make it a particularly useful formalism when using scattered light to measure particle size.
[edit] Mie scattering codes
Mie solutions are implemented in number of codes written in different computer langauges such as Fortran, Matlab, Mathematica. These solutions are in terms of infinite series and include calculation of scattering phase function, extinction, scattering, and absorption efficiencies, and other parameters such as asymmetry of parameter or radiation torque. Current useage of "Mie solution" indicate series approximation to solution of Maxwell's equations. There are several known objects which allow such a solutions: spheres, concentric spheres, infinite cylinders, cluster of spheres and cluster of cylinders, there are also known series solutions for scattering on ellipsoidal particles. For list of these specialized codes examine these articles
- Codes for electromagnetic scattering by spheres - solutions for single sphere, coated spheres, multilayer sphere, cluster of spheres
- Codes for electromagnetic scattering by cylinders - solutions for single cylinder, multilayer cylinders, cluster of cylinders
[edit] Approximations
[edit] Rayleigh approximation (scattering)

Rayleigh scattering describes the elastic scattering of light by spheres which are much smaller than the wavelength of light. The intensity of the scattered radiation is given by
where R is the distance between the particle and the observer, θ is the scattering angle, n is the refractive index of the particle, and d is the diameter of the particle.
It can be seen from the above equation that Rayleigh scattering is strongly dependent upon the size of the particle and the wavelengths. The intensity of the Rayleigh scattered radiation increases rapidly as the ratio of particle size to wavelength increases. Furthermore, the intensity of Rayleigh scattered radiation is identical in the forward and reverse directions.
The Rayleigh scattering model breaks down when the particle size becomes larger than around 10% of the wavelength of the incident radiation. In the case of particles with dimensions greater than this, Mie's scattering model can be used to find the intensity of the scattered radiation. The intensity of Mie scattered radiation is given by the summation of an infinite series of terms rather than by a simple mathematical expression. It can be shown, however, that Mie scattering differs from Rayleigh scattering in several respects; it is roughly independent of wavelength and it is larger in the forward direction than in the reverse direction. The greater the particle size, the more of the light is scattered in the forward direction.
The blue colour of the sky results from Rayleigh scattering, as the size of the gas particles in the atmosphere is much smaller than the wavelength of visible light. Rayleigh scattering is much greater for blue light than for other colours due to its shorter wavelength. As sunlight passes through the atmosphere, its blue component is Rayleigh scattered strongly by atmospheric gases but the longer wavelength (e.g. red/yellow) components are not. The sunlight arriving directly from the sun therefore appears to be slightly yellow while the light scattered through rest of the sky appears blue. During sunrises and sunsets, the Rayleigh scattering effect is much more noticeable due to the larger volume of air through which sunlight passes.
In contrast, the water droplets which make up clouds are of a comparable size to the wavelengths in visible light, and the scattering is described by Mie's model rather than that of Rayleigh. Here, all wavelengths of visible light are scattered approximately identically and the clouds therefore appear to be white or grey.
[edit] Rayleigh Gans Approximation
The Rayleigh Gans Approximation is an approximate solution to light scattering when the relative refractive index of the particle is close to unity, and its size is much smaller in comparison to the wavelength of light divided by |m − 1|, where m is the refractive index.
[edit] Anomalous diffraction approximation of van de Hulst
Anomalous diffraction approximation is valid for large and optically soft spheres. Extinction efficiency in this approximation is given by
 ,
,
where Q is the efficiency factor of scattering, which is defined as the ratio of the scattering cross section and geometrical cross section πa2;
p = 4πa(n – 1)/λ has a physical meaning of the phase delay of the wave passed through the centre of the sphere;
a is the sphere radius, n is the ratio of refractive indices inside and outside of the sphere, and λ the wavelength of the light.
This set of equations, first described by nan de Hulst (1957). [4].
[edit] Applications
Mie theory is very important in meteorological optics, where diameter-to-wavelength ratios of the order of unity and larger are characteristic of many problems regarding haze and cloud scattering. A further application is in the characterization of particles via optical scattering measurements. The Mie solution is also important for understanding the appearance of common materials like milk, biological tissue and latex paint.
[edit] Atmospheric science
Mie scattering occurs when the particles in the atmosphere are the same size as the wavelengths being scattered. Dust, pollen, smoke and water vapour are common causes of Mie scattering which tends to affect longer wavelengths. Mie scattering occurs mostly in the lower portions of the atmosphere where larger particles are more abundant, and dominates when cloud conditions are overcast.
[edit] Cancer detection and screening
Mie theory has been used to determine if scattered light from tissue corresponds to healthy or cancerous cell nuclei using angle-resolved low-coherence interferometry.
[edit] Particle sizing
Mie theory has been used in the detection of oil concentration in polluted water.[5][6]
[edit] Parasitology
It has also been used to study the structure of Plasmodium falciparum, the most important cause of malaria.[7]
[edit] See Also
- Computational electromagnetics
- Light scattering by particles
- List of atmospheric radiative transfer codes
- Optical properties of water and ice
[edit] References
- ^ J. A. Stratton: Electromagnetic Theory, New York: McGraw-Hill, 1941.
- ^ C. F. Bohren,D.R. Huffmann: Absorption and scattering of light by small particles.New York, Wiley-Interscience,2010 ISBN 3527406646
- ^ G. Mie, "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen," Leipzig, Ann. Phys. 330,377–445(1908)English translation, American translation
- ^ a b H. C. van de Hulst: Light scattering by small particles, New York, John Wiley and Sons, 1957
- ^ He, L (2003). "Rapid in situ determination of total oil concentration in water using ultraviolet fluorescence and light scattering coupled with artificial neural networks". Analytica Chimica Acta 478: 245. doi:10.1016/S0003-2670(02)01471-X.
- ^ Lindner, H (2001). "Measurements on Concentrated Oil in Water Emulsions Using Static Light Scattering". Journal of Colloid and Interface Science 242: 239. doi:10.1006/jcis.2001.7754.
- ^ Serebrennikova, Yulia M.; Patel, Janus; Garcia-Rubio, Luis H. (2010). "Interpretation of the ultraviolet-visible spectra of malaria parasite Plasmodium falciparum". Applied Optics 49 (2): 180. Bibcode 2010ApOpt..49..180S. doi:10.1364/AO.49.000180. PMID 20062504.
[edit] Further reading
- Kerker, M. (1969). The scattering of light and other electromagnetic radiation. New York: Academic.
- Barber, P. W.; Hill, S. S. (1990). Light scattering by particles: Computational methods. Singapore: World Scientific. ISBN 9971508133.
- Mishchenko, M.; Travis, L.; Lacis, A. (2002). Scattering, Absorption, and Emission of Light by Small Particles. New York: Cambridge University Press. ISBN 052178252X.
- Frisvad, J.; Christensen, N.; Jensen, H. (2007). "Computing the Scattering Properties of Participating Media using Lorenz-Mie Theory". ACM Transactions on Graphics 26 (3): 60. doi:10.1145/1276377.1276452.
- Wriedt, Thomas (2008). "Mie theory 1908, on the mobile phone 2008". Journal of Quantitative Spectroscopy & Radiative Transfer 109 (8): 1543–1548. Bibcode 2008JQSRT.109.1543W. doi:10.1016/j.jqsrt.2008.01.009.
[edit] External links
- JMIE (2D C++ code to calculate the analytical fields around an infinite cylinder, developed by Jeffrey M. McMahon)
- Collection of light scattering codes
- www.T-Matrix.de. Implementations of Mie solutions in FORTRAN, C++, IDL, Pascal, Mathematica and Mathcad
- ScatLab. Mie scattering software for Windows.
- Online Mie solution calculator is available, with documentation in German and English.
- Online Mie scattering calculator produces beautiful graphs over a range of parameters.
- phpMie Online Mie scattering calculator written on PHP.
- Mie resonance mediated light diffusion and random lasing