QUESTIONS AND ANSWERS

Solve a set of math problems. Detailed solutions to the problems are provided.

Problem 1: The circumference of a circle is equal to 72 pi. Find the radius of this circle.

Detailed Solution.

Problem 2: The length of a rectangular garden is 2 feet longer than 3 times its width. If the perimeter of the garden is 100 feet, find the width and the length of the garden.

Detailed Solution.

Problem 3: A rectangular field has a length 10 feet more than it is width. If the area of the field is 264, what are the dimensions of the rectangular field?

Detailed Solution.

Problem 4: A company has found that when x units of a product are manufactured and sold, its revenue is given by x ² + 100 x dollars and its costs are given by 240 x + 500 dollars. How many units must be produced and sold to make a profit of 10,000 dollars? (HINT: profit = revenue - costs)

Detailed Solution.

Problem 5: A square has a side 5 centimeters shorter than the side of a second square. The area of the larger square is four times the area of the smaller square. Find the side of eachh square.

Detailed Solution.

Problem 6: Find two numbers whose sum is 26 and whose product is 165.

Detailed Solution.

Problem 7: The area of a rectangle is 15 square centimeters and the perimeter is 16 square centimeters. What are the dimensions of the rectangle?

Detailed Solution.

Problem 8: The sum of two numbers is 20. The larger number is four less than twice the smaller number. What rae the two numbers?

Detailed Solution.

Problem 9: The hypotenuse of a right triangle is 2 centimeters more than the longer side of the triangle. The shorter side of the triangle is 7 centimeters less than the longer side. Find the length of the hypotenuse.

a) What is the relationship between x and y?

b) Write the total area A of the three gardens as a function of x.

c) Find the domain of the function A(x).

d) Complete the table of values shown below by calculating the area A given values of x.

x	A(x)
0
5
10
15
20
25

e) Use the table completed in part d) to approximate the value of x for which A is maximum. You may need to generate more values.

f) Graph A and approximate, from the graph obtained, the value of x for which A is maximum.

g) Find the vertex of the graph of A analytically and use it to find the exact value of x for whcih A is maximum.

h) Compare the values of x for which A is maximum found in part e) numerically, f) graphically and part h) analytically.

i) Compare the three methods.

Solution to Problem :

a) Write the formula for the perimeter.

150 = 6 x + 4 y

b) The total area is given by

A = 3 x y

We solve 150 = 6 x + 4 y for y.

y = (75 - 3 x) / 2

Substitute y by (75 - 3 x) / 2 in the formula for the area to obtain.

A(x) = 3 x (75 - 3 x) / 2

c) To determine the domian of A we need to have x, which is a length, positive and also the area must be positive. Hence the two conditions

x > 0 and (75 - 3 x) > 0

Solve the above inequalities to obtain the domain as the interval

(0 , 25)

d) Use the values of x in the formula of the area A(x) and complete the table.

x	A(x)
0	0
5	450
10	675
15	675
20	450
25	0

e) Exdamining the above table, it seems that the maximum is somewhere between 10 and 15. Let us find some more values of A for x between 10 and 15.

x	A(x)
10	675
11	693
12	702
13	702
14	693
15	675

The above values suggest that the value of x that makes A maximum is somewhere between 12 and 13 and may be approximated by 12.5.

f) The graph of A(x) is shown below.

.

From the graph it seems that the value of x that makes A maximum is somewhere between 10 and 15. It can be approximated by 12.5

g) A(x) is a quadratic function which may be written as

A(x) = -(9 / 2) x ² + (225 / 2) x

For a quadratic function of the form ax ² + bx + c, the vertex (h , k) of its graph is given by

h = - b / 2a

When applied to A, h is given by

h = -(225/2) / 2(-9/2) = 12.5

Since the leading coefficient of A(x) is negative, the vertex is a maximum point and therefore the exact value of x that makes A maximum is equal to h = 12.5

h) The numerical and graphical methods gave only approximations to the value of x that makes A maximum: around 12.5 however the analytical method gave the excat value of 12.5

i)
1) Using a computer, the numerical and graphical methods may be easily used to obtain an answer to the problem. However the analytical method needs some work to be done analytically.

2) There are many problems that cannot be solved analytically. However numerical and graphical methods have a wider use in problem solving.

3) Many of the analytical methods give the exact answer however numerical and graphical methods give approximate answers. 

Free-Body Diagrams

1. A book is at rest on a tabletop. Diagram the forces acting on the book. See answer.
   
2. A girl is suspended motionless from the ceiling by two ropes. Diagram the forces acting on the combination of girl and bar. See answer.
   
3. An egg is free-falling from a nest in a tree. Neglect air resistance. Diagram the forces acting on the egg as it is falling. See answer.
   
4. A flying squirrel is gliding (no wing flaps) from a tree to the ground at constant velocity. Consider air resistance. Diagram the forces acting on the squirrel. See answer.
   
5. A rightward force is applied to a book in order to move it across a desk with a rightward acceleration. Consider frictional forces. Neglect air resistance. Diagram the forces acting on the book. See answer.
   
6. A rightward force is applied to a book in order to move it across a desk at constant velocity. Consider frictional forces. Neglect air resistance. Diagram the forces acting on the book. See answer.
   
7. A college student rests a backpack upon his shoulder. The pack is suspended motionless by one strap from one shoulder. Diagram the vertical forces acting on the backpack. See answer.
   
8. A skydiver is descending with a constant velocity. Consider air resistance. Diagram the forces acting upon the skydiver. See answer.
   
9. A force is applied to the right to drag a sled across loosely packed snow with a rightward acceleration. Diagram the forces acting upon the sled. See answer.
   
10. A football is moving upwards towards its peak after having been booted by the punter. Diagram the forces acting upon the football as it rises upward towards its peak. See answer.
    
11. A car is coasting to the right and slowing down. Diagram the forces acting upon the car. See answer.
    

Momentum questions

1. Thrust SSC is a supersonic car powered by 2 jet engines giving a total thrust of
180 kN.
Calculate the impulse applied to the car when the engines run for 4 seconds.


Assume the thrust is the only force acting on the car, which has a mass of 10 000 kg.
Calculate the increase in speed of the car after the 4 s.
2. One suggestion for powering spacecraft engines of the future is an ion engine. A beam of ions (charged atoms) is fired backwards, propelling the spacecraft forwards. In one test, xenon ions were used.
Consider how using xenon ions would compare with using krypton ions, which are lighter.
If equal numbers of each ion were propelled back per second, at the same speed, which type of ion would you expect to give more thrust? Explain your answer




The mass of a xenon ion is 2.2 ´ 10–25 kg, and it can be ejected at a speed of
3.1 ´ 104 m s–1.
Calculate the number of ions that would have to be emitted per second to generate a thrust of 0.1 N (a typical value of the thrust from such an engine).



3. When holding a hose fire-fighters need to ensure that they are not pushed backwards, especially if the water is ejected at a high speed.
Explain why fire-fighters experience a backwards force.




20 kg of water is ejected horizontally in 10 s; the speed of the water leaving the nozzle is 30 m s–1.
Calculate the force experienced by a fire-fighter holding the hose.




4. A spacecraft is approaching the planet Zog and needs to slow down. To do so it fires a jet of gas forwards.
Explain how firing gas forwards slows the rocket down.




The rocket has a mass of 50 000 kg. The gas can be fired forward at a speed of
5 000 m s–1 relative to the rocket.
Calculate the mass of gas must the rocket eject to reduce its speed by 5 m s–1. Ignore the change in the rocket’s mass due to the ejection of gas.




5. Air of density 1.3 kg m–3 strikes a sail of area 15 m2. The air is initially moving at 5 m s–1, assume it is brought to rest when it hits the sail.
Calculate the mass of air is brought to rest in each second?





Hence calculate the average force the air exerts on the sail.




6. A kestrel is a bird of prey which searches for prey by hovering above grassy areas.
Using your ideas about momentum, suggest how a kestrel is able to hover.




The kestrel has a mass of 200 g and it pushes down a column of air of area 600 cm2.
Estimate the downward speed given to the air by the kestrel
g to be 9.8 N kg–1, density of air = 1.3 kg m–3.





Estimate the minimum power the kestrel needs to hover?





Suggest why there are no large birds which can hover? (Some large birds, such as buzzards and condors, may appear to hover, but are not really doing so. They use upwards currents of air – ‘thermals’ – to stay up.)

7. 25 kg s-1 of air at 120 m s-1 is taken in by a jet engine that burns 1 kg fuel each second.
The exhaust gasses are ejected at 520 m s-1 relative to the engine.
a) Calculate the velocity change of the air.


b) Calculate the momentum change per second of the air and also of the fuel.


c) What is the thrust of the jet engine?


8. The H-3 Sea King Helicopter has a mass of about 5400 kg (including crew). It is hovering over the sea on a rescue mission. The rotors have a radius of about 10 m. Air density is 1.2 kg m-3. Assume g = 10 N kg-1
a) What lift force is needed to keep the helicopter hovering?

b) What downward velocity is given to the air by the hovering helicopter?


9. In June 1999, the ESA space probe Giotto made an Earth fly-by following missions to investigate Halley’s Comet in 1986 and Comet Grigg-Skjellerup in 1992. A major hazard to Giotto was the large number of high-speed solid particles (‘dust’) that make up comets’ tails. At collision speeds likely to occur, a 0.1 g particle can penetrate an aluminium plate 8 cm thick. To protect the probe’s instruments, engineers designed a dust shield of two protective sheets 23 cm apart. The front shield is a sheet of aluminium 1 mm thick which retards and vaporises all but the largest particles. The rear shield is a 12 mm thick sheet of Kevlar (as used in bullet-proof vests) which traps any remaining debris and becomes heated as a result.
The Giotto probe has a mass of 960 kg. Suppose it is travelling at 2.0 km s-1 when it encounters a ‘dust’ particle of mass 0.10 g travelling at 50 km s -1 in the opposite direction to the probe. The particle is trapped in the shield.

a) Show that the collision has a negligible effect on Giotto’s velocity.


b) If the collision takes 1.0 ms, calculate the average force exerted on the probe.


c) Explain whether this is an elastic or an inelastic collision.


Answers and Worked Solutions
1.

2. Xenon ions would provide more thrust. This is because there would be a greater momentum change per second since they have a greater mass than krypton ions. Let
m = mass of each ion, n = number of ions emitted per second, v = speed of ejection of ions.
Then, impulse, F D t = change in momentum = (m n) (v – 0): so

3. The pump pushes the water forwards, which by Newton’s third law exerts a force of equal size back on the hose and the pump system. The hose, gripped by the fire-fighter, exerts a backward force on the fire-fighter.

4. To eject the gas, the rocket exerts a forward force on the gas. By Newton’s third law, the gas exerts a force of equal size back on the rocket. This force is responsible for the deceleration of the rocket.



Dm = mass of air brought to rest per second,
v = initial speed of air,
A = area of sail,
r = density of air:


6. The kestrel pushes down on the air, giving it downward momentum. The air pushes back up on the kestrel’s wing (by Newton’s third law). If this upward push equals the weight of the kestrel, the bird can hover at a constant vertical velocity of 0 m s–1.
v = downward speed gained by air, r = density of air, A = area of air column pushed down, mb = mass of bird:
For the bird to hover, the push of the air must equal mb g, the weight of the bird.



7. a) Velocity change of the air = (520 -120) = 400 m s-1
b) Momentum change per second of the air = 25 x 400 = 10,000 kg m s-2
Momentum change per second of the fuel = 1 x 520 = 520 kg m s-2
c) Engine thrust = total momentum change/second = 10,000 + 520 =
10,520 N


8. a) Force is needed to keep the helicopter hovering = weight = 5400 x 10 = 54000 N












b)

9. a) Initial momentum, p = 960 kg x 2.0 x 103 m s-1 – (1.0 x 10-4 kg x 50 x 103 m s-1)
= 1.920 x 106 kg m s-1 – (5.0 kg m s-1 so about 1.920 x 106 kg m s-1)
Final mass, m = 960 kg + 1.0 x 10-4 kg so about 960 kg
Final velocity, v = p/m Since p and m are extremely close to Giotto’s initial mass and velocity, Giotto’s final velocity must be extremely close to its initial velocity.
b) Dust: Dv = 50 - (-2) = 52 km s-1
= (1.0 x 10-4 x 52 / 1 x 10-3 = 5.2 N
c) Collision is inelastic.
Trapping dust results in heating of the shield, so there must be a loss of kinetic energy from the dust.

External References
Questions 1-6: are taken from Advancing Physics Chapter 11, 180S
Question 9: This is taken from Salters Horners Advanced Physics, Section TRA, Additional sheets 8 and 9

 

Check Your Understanding

Use your understanding of the work-energy theorem to answer the following questions. Then click the button to view the answers.
1. Consider the falling and rolling motion of the ball in the following two resistance-free situations. In one situation, the ball falls off the top of the platform to the floor. In the other situation, the ball rolls from the top of the platform along the staircase-like pathway to the floor. For each situation, indicate what types of forces are doing work upon the ball. Indicate whether the energy of the ball is conserved and explain why. Finally, fill in the blanks for the 2-kg ball.


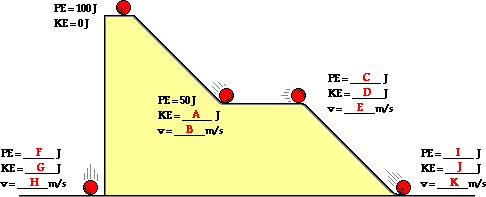
2. If frictional forces and air resistance were acting upon the falling ball in #1 would the kinetic energy of the ball just prior to striking the ground be more, less, or equal to the value predicted in #1?


Use the following diagram to answer questions #3 - #5. Neglect the affect of resistance forces.
3. As the object moves from point A to point D across the surface, the sum of its gravitational potential and kinetic energies ____.

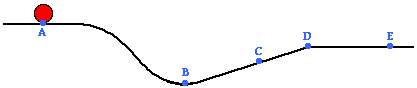
a. decreases, only	b. decreases and then increases
c. increases and then decreases	d. remains the same

4. The object will have a minimum gravitational potential energy at point ____.

a. A

b. B

c. C

d. D

e. E

5. The object's kinetic energy at point C is less than its kinetic energy at point ____.

a. A only

b. A, D, and E

c. B only

d. D and E

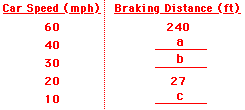
6. Many drivers' education books provide tables that relate a car's braking distance to the speed of the car (see table below). Utilize what you have learned about the stopping distance-velocity relationship to complete the table.


7. Some driver's license exams have the following question.

A car moving 50 km/hr skids 15 meters with locked brakes. How far will the car skid with locked brakes if it is moving at 150 km/hr?

 

8. Two baseballs are fired into a pile of hay. If one has twice the speed of the other, how much farther does the faster baseball penetrate? (Assume that the force of the haystack on the baseballs is constant).

9. Use the law of conservation of energy (assume no friction) to fill in the blanks at the various marked positions for a 1000-kg roller coaster car.




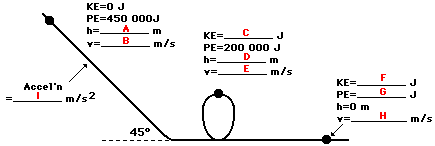
10. If the angle of the initial drop in the roller coaster diagram above were 60 degrees (and all other factors were kept constant), would the speed at the bottom of the hill be any different? Explain.

11. Determine Li Ping Phar's (a mass of approximately 50 kg) speed at locations B, C, D and E.




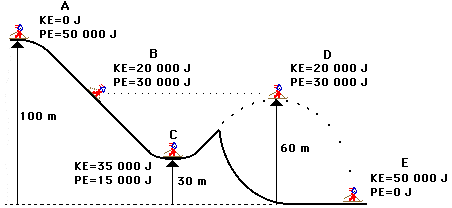
12. An object which weighs 10 N is dropped from rest from a height of 4 meters above the ground. When it has free-fallen 1 meter its total mechanical energy with respect to the ground is ____.

a. 2.5 J

b. 10 J

c. 30 J

d. 40 J

13. During a certain time interval, a 20-N object free-falls 10 meters. The object gains _____ Joules of kinetic energy during this interval.

a. 10

b. 20

c. 200

d. 2000

14. A rope is attached to a 50.0-kg crate to pull it up a frictionless incline at constant speed to a height of 3-meters. A diagram of the situation and a free-body diagram are shown below. Note that the force of gravity has two components (parallel and perpendicular component); the parallel component balances the applied force and the perpendicular component balances the normal force.
Of the forces acting upon the crate, which one(s) do work upon it?

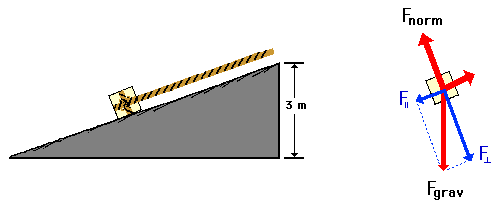
Based upon the types of forces acting upon the system and their classification as internal or external forces, is energy conserved? Explain.

Calculate the amount of work done upon the crate.